2025.05.20 2025.05.21

Diffie-Hellman鍵交換とは

doiken

先日、管理しているネットワーク環境において、IPSec-VPNの接続不安定の障害が発生しました。Diffie-Hellman groupの設定に一因があり、障害の対応としてはパラメータの値さえ正しいものにすれば解決しましたが、そもそもDiffie-Hellman groupとは何のグループなのでしょうか？

Contents

Diffie-Hellmanとは
Diffie-Hellman鍵交換プロトコルの仕組み
Diffie-Hellman鍵交換のリスク＝中間者攻撃
まとめ

Diffie-Hellmanとは

「Diffie-Hellman」というのは、鍵交換のプロトコルの名称です。
そして、そのパラメータのDiffie-Hellman groupは、通信の暗号化の強度を表しており、グループの設定値に比例してセキュリティ強度が高くなるそうです。であれば、単純に一番高い値にしておけば良いのではという気がしますが、強度の高さに反比例して計算処理時間が延び、CPU使用率が高まったり、VPN接続の確立までに時間がかかったりもするそうです。また、対向するネットワーク機器が必ずしも同じ最高値のグループを設定可能とは限りません。

直接的に障害の原因となったDiffie-Hellman groupについては少しわかりましたが、そもそもこの鍵交換のプロトコルはどのような仕組みなのでしょうか？

目的としては、共通鍵交換のための物です。共通鍵の交換は、多くの認証プロトコル(SSH、TLS等)の前提として、通信を開始するお互いで鍵を交換し合います。

Diffie-Hellman鍵交換プロトコルの仕組み

太郎と一郎が鍵交換を行う手順は以下のようになります。
また、第三者のアーノルドは通信の盗聴を狙っています。

まず２つの数字g, nを以下のルールで選びます。
- n: 十分に大きい素数(2048ビット以上が望ましい)
- g: nに対する原始根であることが理想(必ずしもそうでなくても良い様だが、説明は省略)
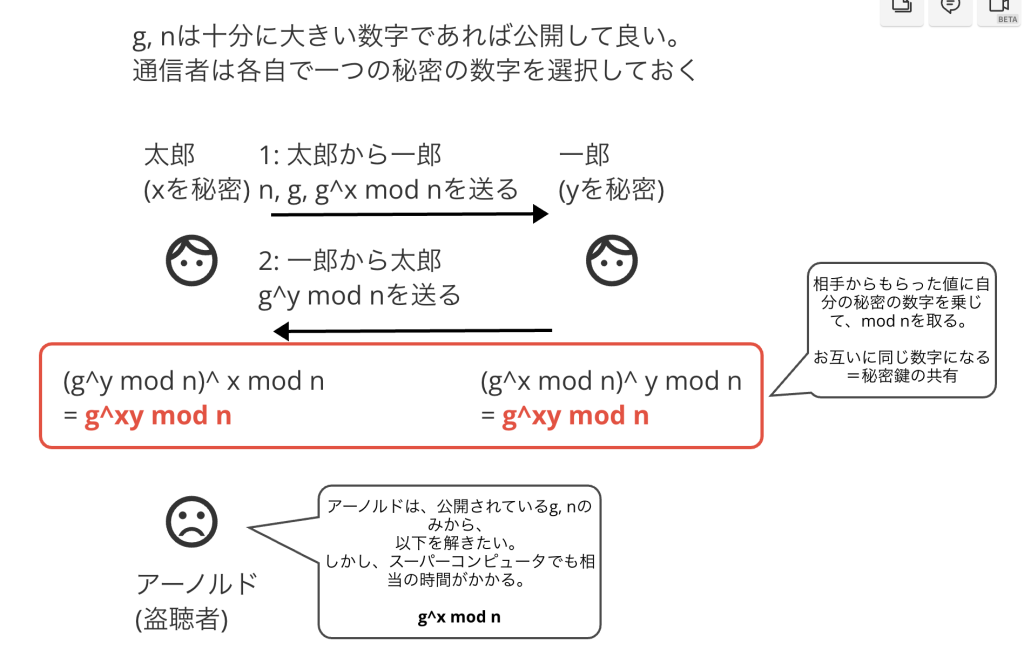
太郎は好きな数字xを選び、g, nとともにg ^x mod n を一郎に送る。
一郎は好きな数字yを選び、太郎から受け取ったg, nを用いて、g^y mod n を太郎に送り返す。
太郎と一郎はそれぞれ、受け取った値に自身の秘密の数字を乗じてmod nを取り、共通となる秘密鍵を得る。
- (g^y mod n) ^x mod n = g^xy mod n
- ( g^x mod n)^y mod n = g^xy mod n

不思議な様ですが、g, nの数字は公開しており（アーノルドにも知られている）、秘密とするのが各自で持っているx, yのみであるにもかかわらずお互いに秘密鍵（g^xy mod n）の交換に成功しました。

ここで、アーノルドは公開されているg, nから g^x mod n または g^y mod nのx, y を解く計算を試みても、スーパーコンピュータでも現実的でない月日がかかります。（g, nをそれぞれ、上述した条件に合致する数字としている場合）また、スマートに計算する方法も現在では見つかっていません。

Diffie-Hellman鍵交換のリスク＝中間者攻撃

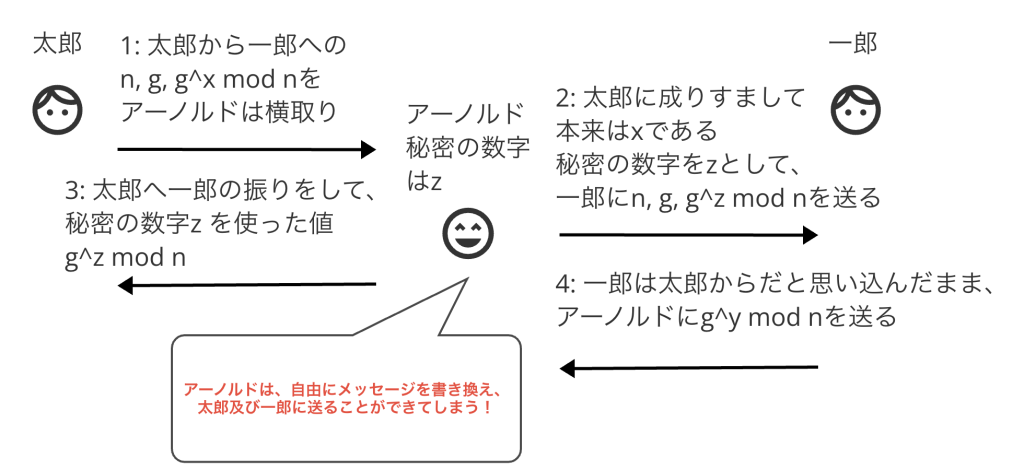
さて、第三者に盗聴可能な状況においてもそのまま安全に鍵交換ができるという不思議で、素晴らしいこのプロトコルにも、だからこそ存在するリスクがあります。それは中間者攻撃です。

Diffie-Hellman鍵交換プロトコルには認証の仕組みがありません。解読の難しい秘密鍵を生成し、交換することには長けていますが、誰から送られてきた鍵情報か、を担保していないため中間者に盗聴されると、簡単に成りすまされてしまうとのことです。

そうすると、結局情報を公開しながら鍵を交換できるといっても、元も子もない様に思えますが...... 実際はSSHやTLSなど、別途認証の仕組みを持つプロトコルとセットで使われています。Diffie-Hellmanだけでは危険ですが、他のプロトコルと組み合わせることで有用な技術として利用されています。