ループ不変条件を意識してプログラムを書く―――二分探索を例に――

最近、社内勉強会でHoare論理というものを学びました。その中で普段プログラムを書く中で意識すると良いなと思う概念として、事前条件、事後条件、不変条件、停止条件といったものがありました。この記事ではループにおいて不変条件を意識することが正確なプログラムを自信を持って書く助けになることを説明したいと思います。

記事の主題からは逸れますがHoare論理について補足します。名前に聞き馴染みがないという方も多いかと思いますし、自分も最近まで存在を知りませんでしたが、実はHoare論理の基本的な考え方は様々なプログラミング設計の方法論に引き継がれているようです。例えば有名なSOLID原則のLに相当するリスコフの置換原則も、Hoare論理の考えを念頭において述べられたもので、事前条件や事後条件といった概念の理解なしに正確に理解することはできないと思われます。他にも契約プログラミングはHoare論理をオブジェクト指向プログラミング向けに発展させたものという見方もできそうです。このように、Hoare論理そのものの名前を聞くことは少なくとも、そのエッセンスは色々なところに引き継がれているようです。

事後条件、不変条件、停止条件の関係

forやwhileなどのループを含むプログラムを書く際、

• 事後条件:ループが終わった時にTrueになっていなければならない条件。ループ終了後にどのような状態になっていて欲しいかを記述する。
• 不変条件:ループの開始前にTrueであり、ループ中とループ終了後に一貫してTrueであり続ける必要のある条件。
• 停止条件:ループが停止する条件。Trueになった時ループが終わる。

というものを意識することでプログラムの満たすべき性質が明確になり、ミスを減らすことができます。

３つの条件の間には以下の関係が成り立ちます。

不変条件 && 停止条件 = 事後条件 ※

上記から、事後条件から停止条件を取り除くことで不変条件が得られるということがわかります。

抽象的な話でわかりにくいと思うので、次節では具体的なプログラムを例に何がそれぞれの条件になるのかを見てみます。

※「不変条件 && 停止条件 ⇒ 事後条件」のみ成り立つ、つまり事後条件の方が弱くても問題ないケースも考えられる気がしますが話を簡単にするためにこれで進めます

具体例

以下のような簡単なプログラムを考えます。xをyで割って、商と余りを返すだけの簡単な関数です。まず余り(remainder)をxで初期化し、ループの中で商をインクリメントしつつ余りからyを減じていき、yが余りよりも小さくなったら終わりです。

def divide_x_by_y(x, y):
    remainder = x
    quotient = 0
    while remainder >= y:
        remainder, quotient = remainder - y, quotient + 1

    # 事後条件
    assert x == quotient * y + remainder and 0 <= remainder and remainder < y
    return quotient, remainder

#事後条件とコメントしている箇所に、事後条件を記載しています。事後条件は以下の3つの条件をandで結んだものになっていますね。

1. x = quotient * y + remainder (割り算として成立するための条件)
2. 0 <= remainder (余りは0以上）
3. remainder < y (余りは割る数未満。そうでなければまだ割れる）

これらの事後条件はこの関数の実行を終えたときに満たしているべき条件であり、割り算とはどうあるべきかを表現しています。事後条件はプログラムの仕様の一部といえます。

事後条件はわかりましたが、不変条件と停止条件は何になるでしょうか。先程の不変条件 && 停止条件 = 事後条件という式は、不変条件と停止条件を合わせる(and)と、事後条件になるということを意味しています。したがって、事後条件①~③のうちいくつかが不変条件、残りのいくつかが停止条件という風に分けることができます。実際のところ、①と②が不変条件、③が停止条件になります。なぜでしょうか。

停止条件はプログラムの中から簡単に見つかります。whlie文を見ればわかるようにループの継続条件がremainder >= yですから、これが成り立たなくなる条件、つまりその否定であるremainder < yが停止条件です。③が停止条件だということになります。

不変条件はプログラム中に明示的に現れていません。事後条件から停止条件を除いた残り、つまり①と②が不変条件と考えていいでしょう。もしループの処理中で不変条件が破られてしまった場合、事後条件の①と②を満たすことができないため、この関数は仕様を満たさないことになります。したがって、ループの中で実行する処理(今回で言えばremainder, quotient = remainder - y, quotient + 1の部分)は不変条件を守るように注意する必要があります。

実際、このプログラムが不変条件を守っていることを確認してみます。①と②はremainder, quotient = remainder - y, quotient + 1という処理を実行してもFalseになることがありません。①については、

x == quotient * y + remainder

に、remainder, quotient = remainder - y, quotient + 1という代入を行ってみると、

x == (quotient + 1) * y + (remainder - y)

となりますが、これは計算してみると元の式と同じであることがわかります。つまり上記の代入文は何度実行しても①がFalseになることはありません。②の方はもっと直感的に、remainder >= y(ループの継続条件)が成り立っている状況下でremainder = remainder - yという代入を行ってもremainderが0未満になることはないということからわかります。

二分探索を考える

ここまででループにおける事後条件、不変条件、停止条件の間に成り立つ関係を見てきました。これらの条件を明確にし、特に不変条件を意識することで二分探索を書く際に起こりがちなインデックスの移動や区間の取り間違いによるバグを防げるということを説明します。

二分探索の問題の例として、なんでも良いのですが以下を考えます。

https://leetcode.com/problems/search-insert-position/description/

問題の概要としては、整数のソート済み配列(値の重複なし)とターゲットの整数が与えられるので、ターゲットの数が配列にもともと存在する場合はそのインデックス、存在しない場合はソートを保ったままターゲットを挿入できる最大のインデックスを返すというものです。例えば配列が[1,3,5,6]の場合、ターゲットが5であれば出力は2、ターゲットが2であれば出力は1となります。

コード例はPythonで示します。実際のところbisectモジュールを使うだけで解けるのですが、これは練習なので自分で探索のコードを書きます。二分探索と言えばなんか探索範囲の真ん中をターゲットと比較して、毎回探索範囲を半分にしていくんだよな〜ということでなんとなく下のようなコードを書いたとします。

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left = 0 # 0からでいいのか？
        right = len(nums) - 1 # ここからでいいのか？

        while left < right: # 等号いらない？
            middle = (right + left) // 2
            if nums[middle] <= target: # 等号いる？
                left = middle # +1とかいらない？
            else:
                right = middle  # +1とかいらない？
        return right # rightでいい？

コメントにも書いてある通り、なんとなく書くとかなり自信がない感じになりがちです。実際このコードは正常に動作しません。どうすればコメントに書いたような点で迷わずに済むのでしょうか。

事後条件を整理する

まずはこの二分探索の事後条件を考えたいです。そのためにはこの二分探索がどう終わるべきなのかを明確にする必要があります。上記のコードでは最後にrightを返しているので、これを踏襲してrightに返すべきインデックスを格納するとします(leftでも解けます)。ループ終了後のrightの位置はどうなるべきでしょうか？左右のインデックスが段々近づいてきて探索範囲がそれ以上なくなったら終わるというのが二分探索の動作なので、leftのすぐ近くにあるはずです。rightの最終位置については、leftと同じ位置/leftの右隣/leftの左隣のどれでも解けるのですが、今回はleftの右隣に来たら終わりということにします。先程の[1,3,5,6]から5を探す例なら、以下のようになって終わりということです。

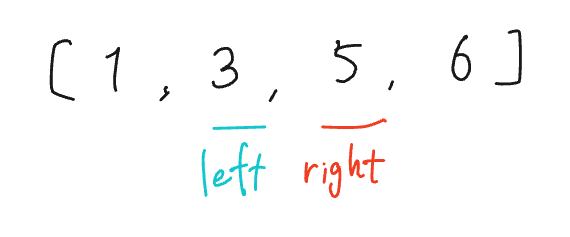
さて、この際の事後条件はどのようなものになるでしょうか。今回の二分探索は、ターゲットが配列内にある時はターゲットの値を返し、無い場合はターゲットよりも大きい最小の要素のインデックスを返すという動作です。つまり、rightがtarget以下の最大の数を指していなければいけません。leftとrightの位置がこれを満たすには、次のような条件を課さなければいけません。

1. rightがleftの右隣
   • left = right - 1
2. left以前の値はターゲット未満でないといけない
   • \(\forall i \leq \, \text{left} \, \text{(nums}[i] \lt \text{target)}\)
3. right以降の値はターゲット以上でないといけない
   • \(\forall i \geq \, \text{right} \, \text{(nums}[i] \geq \text{target)}\)

上記の3条件を満たすと、イメージとしては、leftとrightの間に仕切りがあり、仕切りの左にはターゲット未満の値、仕切りの右にはターゲット以上の値しかないような状態を実現できます。そのような状態であれば、rightが指すのがtarget以下の最大の数になるのは直感的にも理解いただけるでしょうか。

図1の例で①~③が成り立っていることを確認してみます。①は明らかに成り立っています。[1,3,5,6]においてleft以前の位置にある値[1,3]は全てターゲットである5未満になっていることから、②も成り立っています。right以降の値[5, 6]はターゲットである5以上であることから、③も成り立っています。

不変条件と停止条件を考える

さて、ここまでで二分探索の事後条件を定めることができました。ここからは、事後条件をもとに不変条件と停止条件を得たいと思います。「事後条件、不変条件、停止条件の関係」にて述べた通り、不変条件 && 停止条件 = 事後条件が成り立つため、事後条件①~③を不変条件と停止条件に分けることができます。

①〜③のうちのどれを停止条件にし、どれを不変条件とするとプログラムが書けるかを考えます。不変条件と停止条件を選ぶ時、ループの実行前からtrueにできるものが不変条件というのが1つの判断基準です。

①を不変条件にするのは難しそうに思えます。二分探索の探索範囲を表す変数であるleftとrightがループの実行前から隣接した状態にあり、その後その関係が維持されたままでなければならないというのは、二分探索の動作イメージに合いません。これは停止条件になりそうです。

逆に、②と③はループの開始前からtrueにできそうです。leftの初期位置をリスト外の-1としておけば②は確実に満たせます。同様にrightをlen(nums)から始めれば③も満たせます。したがって、

停止条件:①

不変条件:②,③

としてプログラムを考えて行きたいと思います。

初期化~ループの開始まで

上記で言った通り、leftとrightの初期化は-1とlen(nums)で行います。これによって不変条件②と③が満たされます。

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left = -1
        right = len(nums)

次に、whileループの継続条件ですが、これは停止条件①の否定でいいので、left != right -1とします。

while left != right -1:

leftの移動

次はループ内のif文について考えます。真ん中の値(nums[middle])がtargetより大きいなら探索範囲を左半分、小さいなら右半分に絞るというのはわかっていても、nums[middle]==targetの時にどう動かすべきか、新しい探索範囲にtargetを含めるかどうかなど迷いが生じます。

ここで不変条件を明確にしたことが効いてきます。先ほど整理した通り、今回は以下がループの不変条件ですので、これらを守りつつ探索範囲を絞らなければいけません。

• left以前の値はターゲット未満でないといけない
  • \(\forall i \leq \, \text{left} \, \text{(nums}[i] \lt \text{target)}\)
• right以降の値はターゲット以上でないといけない
  • \(\forall i \geq \, \text{right} \, \text{(nums}[i] \geq \text{target)}\)

まずleftを移動するときのことを考えます。もともと書いていたif文は以下の通りでした。

if nums[middle] <= target:
    left = middle

これはよく考えると1つめの不変条件を満たしません。nums[middle]==targetのときにleftにmiddleを代入してしまうと、nums[left]==targetとなってしまうからです。1つめの不変条件からnums[left]はtarget未満でなければいけません。

nums[middle]==targetのケースに問題があるので、if文の条件式から等号を取り除いてみます。

if nums[middle] < target:
    left = middle

これであれば1つめの不変条件を満たします。if文の条件によって既にtarget未満であるとわかっているmiddleの位置にleftを移動すると考えると納得できると思います。ここでmiddle+1などとしてしまうと、targetとの大小関係がわからないところまでleftを進めてしまうので不変条件を破る可能性があることに注意してください。なお、2つめの不変条件にはleftが現れないのでこれは考えるまでもなく満たせます。

このように不変条件を明確にしたことで、複数あるif文の条件式やleftに代入する値の候補から自信を持って選択できました。

rightの移動

次にrightの移動です。もともとのコードではrightの移動は以下のように行っていました。

else:
    right = middle

elseに対応するifの条件式は、先程if nums[middle] < targetとしました。したがって、ここのelseの条件はnums[middle] >= targetですので、以下のように読み替えられます。

if nums[middle] >= target:
    right = middle

この移動は2つ目の不変条件を満たすでしょうか？targetの値以上であるとわかっているmiddleの位置にrightを移動するわけですから、移動後もright以降の値はtarget以上であるままです。したがって不変条件を満たします。

完成

以上のことから、最終的なコードは以下になります。結局、最初のコードとの相違点はif文の条件式の不等号の有無のみとなりました。しかし、ここまでのように考えなければ、最初のコードの間違いを明確な根拠をもって指摘するのはなかなか難しかったのではないかと思います。

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left = -1
        right = len(nums)

        while left != right - 1:
            middle = (right + left) // 2
            if nums[middle] < target:
                left = middle
            else:
                right = middle
        return right

ここで1つ別解を見てみたいと思います。例えば、以下のコードもこの問題の正解になります。

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums) - 1

        while left <= right:
            middle = (left + right) // 2
            if nums[middle] == target:
                return middle
            elif nums[middle] > target:
                right = middle - 1
            else:
                left = middle + 1        
        return left

answer1.pyと比べるとかなり相違点があります。

1. leftとrightの初期値
2. leftとrightの移動する条件(if文の条件式)
3. leftとrightの移動先(middleの後の±1の有無)

など（他にもありますが）、最初に自信のないコードを書いた時にコメントで不安視していた箇所が色々と異なっています。もしanswer2.pyのright = middle - 1をright = middleに変えると正常に動作しませんし、他の箇所も同様です。したがって、①~③の選択は適切な組み合わせでなければいけなかったわけです。（アルゴリズムにものすごく慣れている人はできるかもしれませんが）この選択を感覚的に行うのはなかなか難しいと思います。こういったことを考えると、やはり不変条件を意識することが正確なプログラムを書く助けになっていると思います。

mitchy

SIerで物流システムの保守運用に従事した後、2022年1月にDWSに入社。最近は主にGoでバックエンドの開発をしています。趣味はゲームと散歩。